Problem TRVLCHEF

There are n cities and each city i has temperature c[i]. You can travel from each city i to another city j if |c[i] - c[j]| < d, where d is your temperature change tolerance (which is given). However, you can visit each city only once. Starting at city 1, is it possible to visit all cities (Yes/No)? ¹

An example with d=2 and n=8:

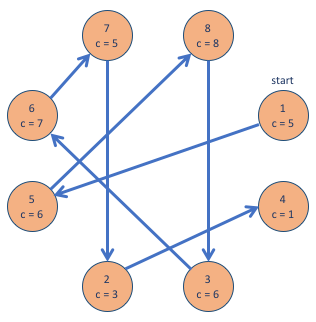
¹ n < 10^5 and there are 1000 test cases. basically, we can’t do worse than O(nlog(n)) per test case.

Observations

Generally, solving Hamiltonian Path is NP-Complete but in this problem we have a very special graph, where only the temperatures matter.

1. There is only one parameter associated with each city (temperature). So, it seems natural to sort them on a line based on their c value.
2. If c[i + 1] - c[i] > d for any i, the graph would be disconnected and we can’t solve it
3. Given 2. is satisfied,
   • if city 1 is the first or the last city in the sorted list, the answer is Yes.
   • if city 1 is somewhere in the middle, an answer is Yes, if and only if we can solve it right-left or left-right. (we define it below)

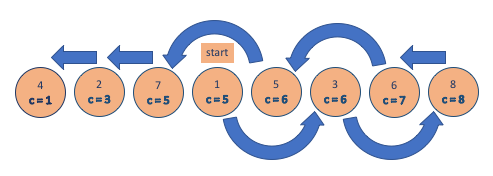
In order to solve right-left, we make jumps of 2 towards right all the way to the end, then jumps of 2 coming back and going past the start city and then we just visit the rest of the cities one by one. (left-right is defined similarly). The image below shows a right-left solution for the previous graph)

Correctness

In order to see why this if and only if holds, first it is trivial that if such a path exists, we have a solution. Now, we need to prove that if the problem has a solution, either a left-right or a right-left solution exists. Let’s prove by contradiction.

Suppose the problem has a solution but neither left-right nor right-left solutions would work. First let’s look at the right-left path. Since a solution exists, we know that after sorting cities by temperature, c[i] - c[i - 1] <= d for every i. So, if the right-left path doesn’t work, somewhere to the right of the start city, for some i we have c[i] - c[i - 2] > d. That means, the only way to reach c[i] from c[i - 2] is going through c[i - 1]. This means once we go from c[i - 2] to c[i], we can’t come back. Because of that if we begin at start and go to right once we visit the last city on the right, we can never come back to visit cities to the left of start. Similarly we can prove the same for the leftmost city using the fact that left-right solution doesn’t work. So, starting from start it is not possible to cover the leftmost city as well as the rightmost city. hence the supposition is false and the statement is true.

Solution

In order to implement the solution, we can check if the right-left solution or the left-right solution would work. In order to check that, all we need to do is:

1. sort cities by their temperature
2. make sure c[i] - c[i - 1] <= d for each i > 0
3. if start_city is the first or the last city in the sorted list, the answer is Yes
4. if start_city is somewhere in the middle, check that for all nodes to the right of it c[i] - c[i - 2] <= d and for all nodes to the left of it c[i + 2] - c[i] <= d.

This solution takes O(nlogn) to sort cities, and O(n) to solve. Note that if the max(|c[i] - c[j]|) ~ O(n), we can use counting sort and bring down the total time to O(n). Also, if d is small we can sort in O(n * d) since if any city’s temperature is more than n * d away from the start city, the answer is No, so we could use counting sort in range (startIdx -/+ n * d).

Code

Here is the solution in Java.

    private static boolean solve(int n, int d) {
        int startValue = c[0];
        Arrays.sort(c, 0, n);

        int startIdx = -1;
        for (int i = 0; i < n; i++) {
            if (startValue == c[i])
                startIdx = i;

            if (i > 0 && c[i] - c[i - 1] > d) {
                return false;
            }
        }

        if (c[0] == startValue || c[n - 1] == startValue)
            return true;

        // consider going left first
        boolean left = true;
        for (int i = 0; i < startIdx && i + 2 < n; i++) {
            if (c[i + 2] - c[i] > d)
                left = false;
        }

        // consider going right first
        boolean right = true;
        for (int i = n - 1; i > startIdx && i - 2 >= 0; i--) {
            if (c[i] - c[i - 2] > d)
                right = false;
        }

        return left || right;
    }