Nima Aghdaii

Rooks on Chessboard

10 Jun 2019 » recursion, heuristic, problems, divide-and-conquer

Problem ADAROKS2

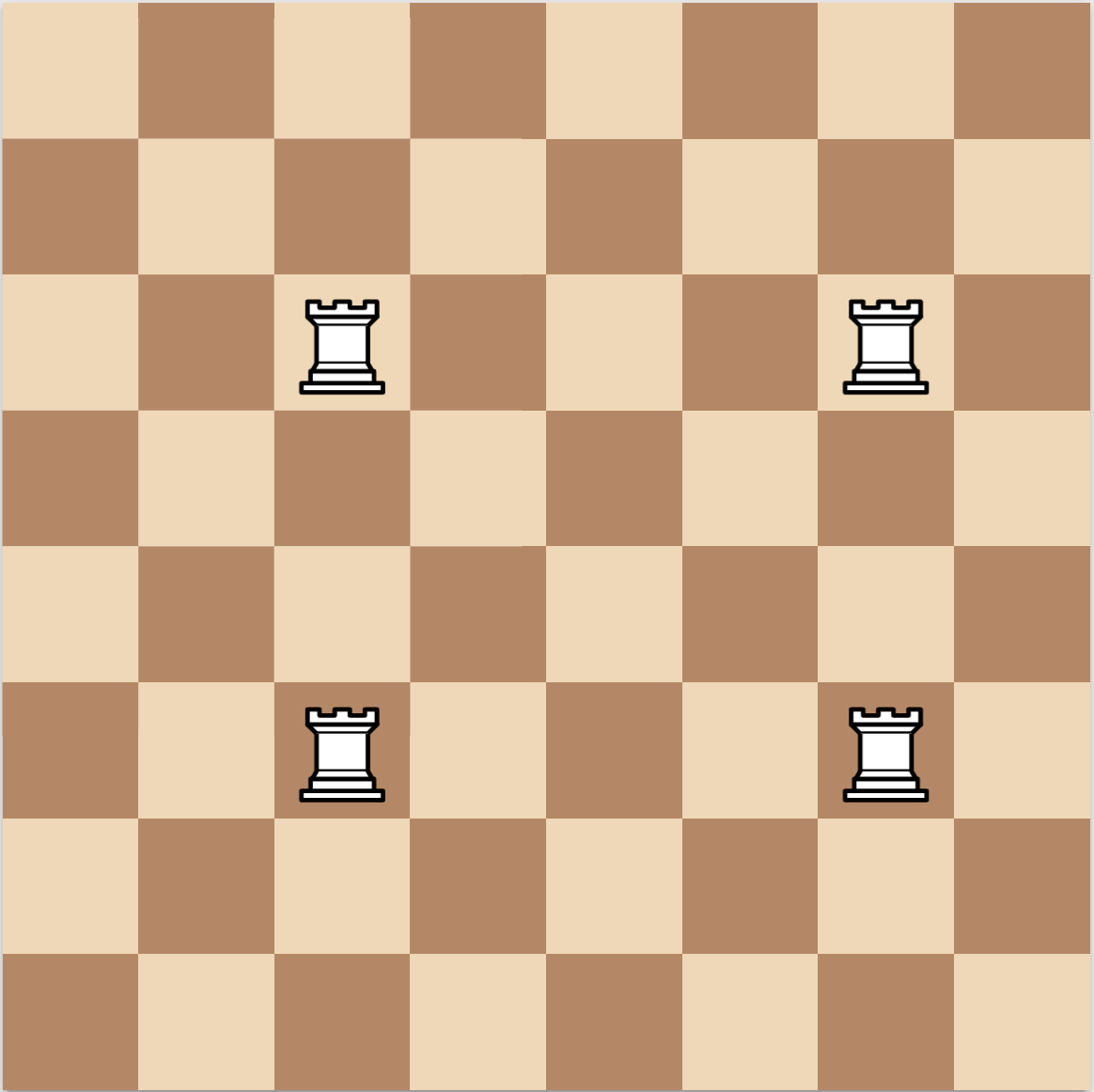
How many rooks can you place on a N x N chessboard such that no four of them form a rectangle? To be more precise, 100 <= N <= 1000 and we need to place 8 * N rooks on the board. Below is an example of rooks forming a rectangle.

prev

Thought Process


Step 1: pen & paper

I couldn’t come up with anything better than 3 * N using the pattern below. Still far away from 8 * N!

OOOOOOO.
O......O
.O.....O
..O....O
...O...O
....O..O
.....O.O
......OO


Step 2: brute force

Then I decided to write some brute-force solution to get the most optimal answer for small values of N. I was hoping I can see a pattern there. This is what I got (for more than 6, it would take a very long time):

2
.O
OO

3
.OO
O.O
OO.

4
..OO
.O.O
O..O
OOO.

5
...OO
..O.O
.O..O
O...O
OOOO.

6
....OO
..OO..
.O.O.O
.OO.O.
O..OO.
O.O..O

Code:

private static void solve(int n, int i, int j, int cnt) {
    if (j >= n) {
        solve(n, i + 1, 0, cnt);
        return;
    }
    if (i >= n) {
        if (cnt > bestCnt) {
            bestCnt = cnt;
            deepCopy(b, best, n);
        }
        return;
    }
    b[i][j] = good(i, j);
    if (!b[i][j]) {
        b[i][j] = false;
        solve(n, i, j + 1, cnt);
    } else {
        b[i][j] = false;
        solve(n, i, j + 1, cnt);
        b[i][j] = true;
        solve(n, i, j + 1, cnt + 1);
    }
}

private static boolean good(int i, int j) {
    for (int k = 0; k < i; k++) {
        for (int l = 0; l < j; l++) {
            if (b[k][l] && b[k][j] && b[i][l])
                return false;
        }
    }
    return true;
}


Step 3: greedy

Unfortunately doing greedy performs really poorly since it will fill up the first row and then you can’t place more than one rook on any other row, otherwise they’ll create a rectangle. However, it seems like if we can somehow fill some of the board more intelligently and then fill the rest using greedy, it would not be too bad.


Step 4: Divide & Conquer

What if we have a good solution for N, can we build a decent solution for 2*N? For example, given the solution for N = 5, we can build the solution below for N = 10.

...OO.....
..O.O.....
.O..O.....
O...O.....
OOOO......
........OO
.......O.O
......O..O
.....O...O
.....OOOO.

This is actually great, because if we have a 8*N solution for some N, this method gives us the solution for N*2 x N*2 board! But can we do better? For example we can simply improve it by also filling one diagonal on one of the small squares:

...OOO....
..O.O.O...
.O..O..O..
O...O...O.
OOOO.....O
........OO
.......O.O
......O..O
.....O...O
.....OOOO.

However, it is not good enough to achieve 8*N for N = 100. Now, what if instead of filling the small diagonal, we let the greedy algorithm run on both small empty squares? However, filling greedy-ly using the code below, actually ends up filling the same diagonal, which is not great.

for (int i = 0; i < n; i++) {
    for (int j = 0; j < n; j++) {
        if (!ans[i][j] && possibleToFill(ans, i, j, filled)) {
            ans[i][j] = true;
            filled.add(point(i, j));
        }
    }
}


Step 5: Divide & Conquer + Guided Greedy

The trick to solve this problem was the realization that if you start filling squares where we have more degrees of freedom (sparse areas), you tend to achieve worse results compared to if you try to fit rooks in denser areas. So, I simply changed the order in which we check cells by looking at the main diagonal first, then the two smaller semi-diagonals next to it and slowly walking away in both directions. Something like this:

for (int i = n; i >= 1; i--) {
    for (int j = 0; j < i; j++) {
        int offset = n - i;
        int ii = j;
        int jj = offset + j;
        if (ii < n - 1 && jj < n - 1 && ((ii < n1 && jj < n1) || (ii >= n1 && jj >= n1))) continue;
        if (!ans[ii][jj] && possibleToFill(ans, ii, jj, filled)) {
            ans[ii][jj] = true;
            filled.add(point(ii, jj));
        }
        if (!ans[jj][ii] && possibleToFill(ans, jj, ii, filled)) {
            ans[jj][ii] = true;
            filled.add(point(jj, ii));
        }
    }
}

With this simple change, for N = 10, we get this board:

...OO.....
..O.O.....
.O..O..O..
O...O.O...
OOOO.O....
....O...OO
...O...O.O
..O...O..O
.....O...O
.....OOOO.

You may think just one more rook? But as N grows the difference becomes more significant. For example, for N = 50, we get this board:

....OO......O...................O.....O...........
..OO.......O..............O.......................
.O.O.O...........O............................O...
.OO.O.....O...........O......O....................
O..OO...O...........O..................O..........
O.O..OOO.......O....................O.............
.....O....OO...................O...............O..
.....O..OO.........O......O.................O.....
....O..O.O.O...............O......................
.......OO.O.....O.O..................O............
...O..O..OO...O.........O....................O....
.O....O.O..OOO.......O...........................O
O..........O....OO......O.......................O.
...........O..OO.......O.................O........
..........O..O.O.O.......O.................O......
.....O.......OO.O.....O.....O.....................
.........O..O..OO...O............O......O.........
..O.........O.O..OOO...................O..........
.........O.......O....OO.............O............
.......O.........O..OO......O...O.................
....O...........O..O.O.O.O.........O..........O...
...........O.......OO.O.......O............O......
...O...........O..O..OO....O..........O...........
.............O....O.O..OO......O............O.....
.......O....O.........O.OOO.......O...............
.....O...............O..O....OO......O............
.O.................O....O..OO.......O.............
O.........O............O..O.O.O...........O.......
..............O.....O.....OO.O.....O...........O..
...........O......O......O..OO...O...........O....
..O.....O................O.O..OOO.......O.........
.........O........O...........O....OO.............
....O.O..........O............O..OO.........O.....
...O...................O.....O..O.O.O.............
........................O.......OO.O.....O.O......
...............O............O..O..OO...O.........O
..........................O....O.O..OOO.......O...
....................O....O..........O....OO......O
......................O.............O..OO.......O.
.................O.................O..O.O.O.......
.O..............O.............O.......OO.O.....O..
O............O.....O..............O..O..OO...O....
...........................O.........O.O..OOO.....
..O......O...........O............O.......O....OO.
......................O.........O.........O..OO...
............O................O...........O..O.O.O.
....................................O.......OO.O..
......O.....................O...........O..O..OO..
.......O...............O..............O....O.O..OO
................................O....O.........O.O


Final Solution

Eventually, the divide & conquer + guided greedy did a pretty good job and for up to ~200, runs pretty quickly. Beyond that, we can just do the trick from “Step 4” and achieve a quick 8*N solution. Extra optimizations I did to make it work:

  1. memoize the output for each N < 200
  2. compress a pair of integers (each less than 1000) into one integer and use a Set<Integer> to avoid creating pairs.

Here is my code that passed all the tests. The answer for N = 200 looks like this:

N200


Learning

Greedy solutions are often not ideal since they fall into a very simple local minima. However, combining with divide and conquer can sometimes avoid falling into those local minimas. The key point here is the hierarchical structure in which the greedy approach is applied. Also, in certain cases like this case, it makes more sense to fill greedily from denser areas first.

Related Posts