Problem ADAPWN
We are given a NxN chess board and some number of pawns on the board. Every pawn on (i, j) threatens cells (i-1, j-1) and (i-1, j+1) and if there is a pawn on either of these cells, it can capture one of them. The goal is to declare a sequence of captures (note that ordering matters!) such that after captures are performed, no pawn is under a threat by another pawn anymore.
For example, given this starting position:

Here is one optimal sequence of captures:
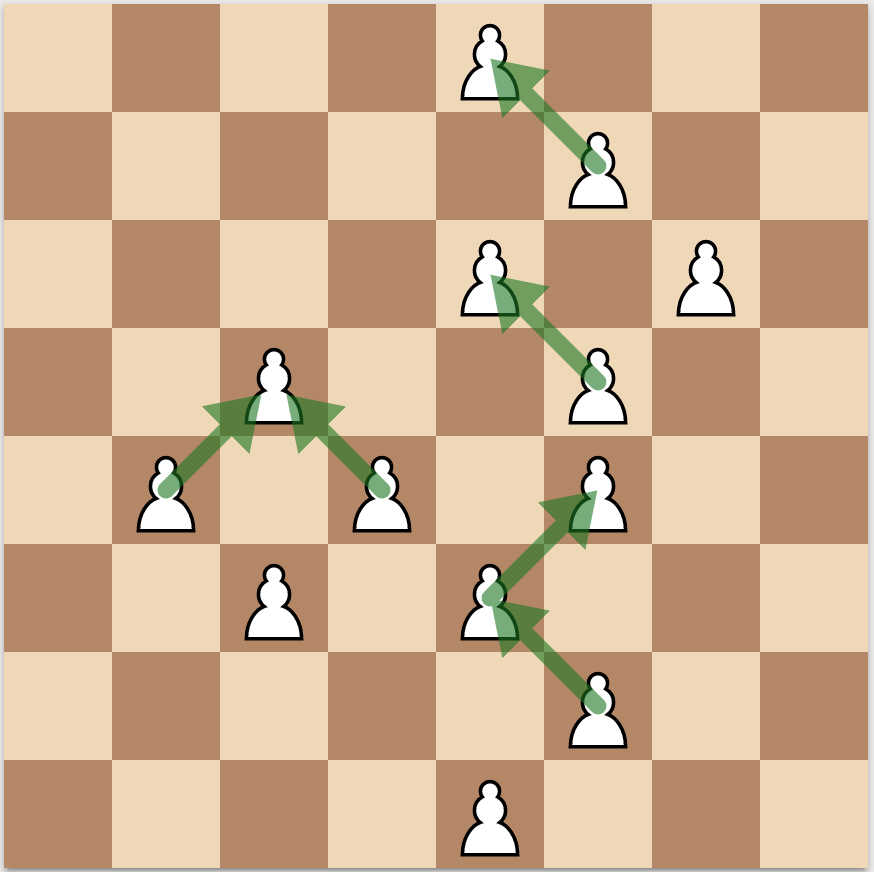
Which results in a no-threat situation:

Example input:
1
8
....O...
.....O..
....O.O.
..O..O..
.O.O.O..
..O.O...
.....O..
....O...
Example output:
6
7 6 L
4 6 L
2 6 L
5 2 R
5 4 L
6 5 R
Note that captures 7 6 L and 6 5 R cannot be reordered!
Ideas
First observation is to think of a capture as removal of a pawn. when pawn p1 captures, pawn p2, it is equivalent of just removing pawn p1. However, if a pawn is not attacking another pawn, it cannot be removed (this made things a bit tricky at the end).
I tried a lot of heuristics, such as eliminating in certain order or going with the highest degree nodes first. But none worked and an example like this made me realize why picking the highest degree pawn is not the best choice:

After trying a few ideas on paper and coding brute-force to try them out, I was almost certain there has to be some sort of optimization to solve this problem.
Game Theory
There is a pretty elegant solution using grundy numbers (aka Nimber). You can read about that solution from the official editorial page here.
Graph Theory
Imagine a graph where each pawn is a vertex and any pawn threatening another pawn is an edge between those two. The objective of this problem is to not have any threats left. Which means, for each edge e = (p1, p2) either p1 or p2 (or both) should be eliminated in such a way that minimum pawns are eliminated in total. This is basically minimum vertex cover, where we need to pick minimum number of vertices such that every edge is adjacent to least one picked vertex. While the vertex cover problem in general is NP-Complete, it can be solved fairly efficiently on a bipartite graph using Kőnig’s Theorem. This page has a pretty good visual explanation of the theorem. Basically, the problem becomes finding the maximum matching on a bipartite graph.
Bi-partite Graph
A graph is bi-partite if it doesn’t have any cycles or all cycles are of even length. You can prove that our graph in this problem is bi-partite by showing it cannot have an odd cycle. Also, if you are into graph theory, you probably know that every planar graph whose faces all have even length is bipartite. However, in this case it is even simpler. Just assign pawns on even rows to one group and pawns on odd rows to another group.
Handling Final Pawns
Notice that for even a simple case where there are two pawns and p1 is threatening p2, you can either eliminate p1 or p2 to eliminate the threat. However, since the problem asks for a “pawn capture”, p2 can’t capture any pawn, and we can only eliminate p1. So, a simple bipartite vertex cover problem wouldn’t be enough since it may pick p2 as the pawn to be removed. In order to cover these cases, imagine a pawn c that doesn’t threaten any other pawn but is threatened by pawns p1, p2, p3. Since c cannot be eliminated, in order to remove the threat, we have to eliminate all p1, p2 and p3. So, we can remove these pawns and all the edges connected to them, to find the vertex cover on the remaining graph. At the end we can add the removed pawns to the final solution.
Solution Overview
- read input and store the grid
- create a parent/child graph where
p1is parent ofp2ifp1attacksp2 - mark any node that has a childless child (and add them to the
must_takeslist) - mark any node that doesn’t have a child
- remove all marked nodes
- use dfs to create a graph of the remaining pawns
- create the bipartite graph
- run bipartite vertex cover and get
coveras minimum pawns chosen - print the list of
cover+must_takesas the final answer
Implementation
def augment(u, bigraph, visit, match):
for v in bigraph[u]:
if not visit[v]:
visit[v] = True
if match[v] is None or augment(match[v], bigraph,
visit, match):
match[v] = u
return True
return False
def max_bipartite_matching(bigraph):
n = len(bigraph)
match = [None] * n
for u in range(n):
augment(u, bigraph, [False] * n, match)
return match
def _alternate(u, bigraph, visitU, visitV, matchV):
visitU[u] = True
for v in bigraph[u]:
if not visitV[v]:
visitV[v] = True
assert matchV[v] is not None
_alternate(matchV[v], bigraph, visitU, visitV, matchV)
def bipartite_vertex_cover(bigraph):
V = range(len(bigraph))
matchV = max_bipartite_matching(bigraph)
matchU = [None for u in V]
for v in V:
if matchV[v] is not None:
matchU[matchV[v]] = v
visitU = [False for u in V]
visitV = [False for v in V]
for u in V:
if matchU[u] is None:
_alternate(u, bigraph, visitU, visitV, matchV)
inverse = [not b for b in visitU]
return (inverse, visitV)
dr = [+1, +1, -1, -1]
dc = [+1, -1, +1, -1]
def add_edge(G, (r, c), (newr, newc)):
if (r, c) not in G:
G[(r, c)] = [(newr, newc)]
else:
G[(r, c)].append((newr, newc))
def dfs((rr, cc), b, G, vis, n, U, V):
stack = [(rr, cc, False)]
while len(stack) > 0:
r, c, parity = stack.pop()
if parity:
U.append((r, c))
else:
V.append((r, c))
for i in range(4):
newr = r + dr[i]
newc = c + dc[i]
if 0 <= newr < n and 0 <= newc < n and b[newr][newc]:
add_edge(G, (r, c), (newr, newc))
if (newr, newc) not in vis:
vis.add((newr, newc))
stack.append((newr, newc, not parity))
def create_graph(b, n):
G = {}
U, V = [], []
vis = set()
for i in range(n):
for j in range(n):
if b[i][j] and (i, j) not in vis:
dfs((i, j), b, G, vis, n, U, V)
if len(U) < len(V):
U, V = V, U
return G, U, V # U is bigger
def create_parchil(b, n):
par = [[] for i in range(n * n)]
chil = [[] for i in range(n * n)]
for r in range(n - 1):
for c in range(n):
if b[r][c]:
if c - 1 >= 0 and b[r + 1][c - 1]:
par[num((r, c), n)].append(num((r + 1, c - 1), n))
chil[num((r + 1, c - 1), n)].append(num((r, c), n))
if c + 1 < n and b[r + 1][c + 1]:
par[num((r, c), n)].append(num((r + 1, c + 1), n))
chil[num((r + 1, c + 1), n)].append(num((r, c), n))
return par, chil
def num((i, j), n):
return i * n + j
def has_childless_child(chil, x):
for cx in chil[x]:
if chil[cx] == []:
return True
return False
def create_bb(b, n, chil):
bb = [row[:] for row in b]
must_takes = []
for i in range(n):
for j in range(n):
x = num((i, j), n)
if has_childless_child(chil, x):
must_takes.append(x)
bb[i][j] = False
if chil[x] == []:
bb[i][j] = False
return bb, must_takes
def create_bigraph(G, U, n):
res = {}
for u in U:
res[num(u, n)] = []
if u in G:
for neigh in G[u]:
res[num(u, n)].append(num(neigh, n))
for i in range(n * n):
if i not in res:
res[i] = []
return res
def print_pawn(p, n, b):
i = p / n
j = p % n
if i > 0 and j > 0 and b[i - 1][j - 1]:
print i + 1, j + 1, 'L'
elif i > 0 and j < n and b[i - 1][j + 1]:
print i + 1, j + 1, 'R'
else:
print i + 1, j + 1, 'X'
b[i][j] = False
def print_solution(cover, b, n, must_takes):
moves = len(must_takes)
for i in range(n * n - 1, -1, -1):
if cover[0][i] or cover[1][i]:
moves += 1
print moves
for i in range(n * n - 1, -1, -1):
if cover[0][i] or cover[1][i]:
print_pawn(i, n, b)
for p in must_takes:
print_pawn(p, n, b)
tc = input()
for t in range(tc):
n = input()
b = []
for i in range(n):
b.append(map(lambda c: c == 'O', list(raw_input())))
par, chil = create_parchil(b, n)
bb, must_takes = create_bb(b, n, chil)
G, U, V = create_graph(bb, n)
bigraph = create_bigraph(G, U, n)
cover = bipartite_vertex_cover(bigraph)
print_solution(cover, b, n, must_takes)