Here are my solutions to Codechef December 2020 Challenge.

Even Pair Sum (EVENPSUM)

Can be done fairly easily in O(1) by counting even and odds.

def odd(x):
    return (x + 1) // 2

def even(x):
    return x - odd(x)

tc = int(input())
for t in range(tc):
    a, b = map(int, input().split())
    res = even(a) * even(b) + odd(a) * odd(b)
    print(res)

✅ Code

Positive Prefixes (POSPREFS)

A simple heuristic would be to just fill numbers alternating + and -:

1 -2 3 -4 5 -6 ...

and at any point consider filling the rest with all - or all +.

✅ Code

Hail XOR (HXOR)

For each operation, we just use XOR to unset the msb (most significant bit) of the leftmost non-zero number in the list. Since we need to apply this operation to the same bit on another number as well, we pick the next number in the list with that bit set. In order to find the next number with the i-th bit set, we can maintain an array where the i-th element stores the index of the leftmost number in the list with the i-th bit set. As we use XOR to unset that bit, we find the next index and update that element of the array in linear time. In total, the runtime will be O(N * BITS). The two corner cases we need to be careful about are: 1) when all elements are zero except the last element. 2) there is only one number with the i-th bit set. For how to handle these details, you can check my code link below.

✅ Code

Calculus (CALCULUS)

I had a lucky/lazy approach to this problem. Assuming \(F(N)\) is: \[\begin{equation} \begin{aligned} F(N) &= \int_{0}^{\infty} \dfrac{ e^{2 \pi x} - 1 }{e^{2 \pi x} + 1} \left( \dfrac{1}{x} - \dfrac{x}{N^2 - x^2} \right) \,dx \end{aligned} \end{equation}\]

From the example test case, we know \(F(1) = 2\). Then you can plug in different values of \(N \in \{2, 3, 4, \cdots \}\) and use WolframAlpha to find the integral from \(0\) to \(\infty\). Here is an example (for \(N=2\)) and below are some more: \[\begin{equation} \begin{aligned} F(1) &= 2 \\ F(2) &= 2.\bar6 = 2 + \frac{2}{3}\\ F(3) &= 3.0\bar6 = 2 + \frac{2}{3} + \frac{2}{5} \\ F(4) &= 3.35238 = 2 + \frac{2}{3} + \frac{2}{5} + \frac{2}{7} \end{aligned} \end{equation}\]

So, the solution is simply: \[F(N) = \frac{2}{1} + \frac{2}{3} + \frac{2}{5} + \cdots + \frac{2}{2N - 1}\]

which you can do with a one liner in python:

def solve(n):
    return sum((2 * mod_inv(2 * i + 1, MOD)) % MOD for i in range(n)) % MOD

✅ Code

String Operations (STROPERS)

Since we can reverse any substring with even 1s in it, a special case is when we have only two 1s in the string with a zero on the left. Reversing this substring results in a left shift: \[01001 \rightarrow 10010\]

By repeating this operation, in any order, on any given string s we get a representative for that class (you can prove it yourself). For example, let’s start with the string \(0100001100110\), we can shift the two leftmost 1s to the left once : \[0\color{magenta}{100001}100110 \\ \color{magenta}{100001}0100110 \\\]

Then we pick the next pair and shift left: \[10000\color{magenta}{101}00110 \\ 1000\color{magenta}{101}000110 \\ 100\color{magenta}{101}0000110 \\ 10\color{magenta}{101}00000110 \\ 1\color{magenta}{101}000000110 \\\]

And the next: \[110\color{magenta}{10000001}10 \\ 11\color{magenta}{10000001}010 \\\]

And the next: \[111000000\color{magenta}{101}0 \\ 11100000\color{magenta}{101}00 \\ 1110000\color{magenta}{101}000 \\ 111000\color{magenta}{101}0000 \\ 11100\color{magenta}{101}00000 \\ 1110\color{magenta}{101}000000 \\ 111\color{magenta}{101}0000000 \\\]

Finally we have the representative of the class: \[R(0100001100110) = 1111010000000\]

The representative string will always look like a group of 1s (potentially none), then a group of 0s (potentially none), one 1, a group of zeros (potentially none). So, we can uniquely identify each representative with the triplet: <num_ones, zeros_between, zeros_after> or simpler: <num_ones, zeros_between, string_length>. However, spending O(N) time to calculate the representative would be too slow. Let’s see if we can calculate them in O(1).

Notice that each shift operation jumps a 0 over the next two 1s. So, if we group consecutive zeros and number them from left to right (group 0, group1, group2, etc.), the sum of odd groups will always stay the same under this operation (same with the even groups). So, we can keep track of odd/even zero groups as we encounter them and update our representative in O(1) as we iterate through substrings.

Finally, we insert all the representatives we find into a set and at the end we look at the size of the set. Here is the code to solve this problem:

def solve(s):
    classes = set()
    for i in range(len(s)):
        z = [0, 0]
        ones = 0
        cur_par = 0
        for j in range(i, len(s)):
            if s[j] == '1':
                ones += 1
                cur_par = 1 - cur_par
            else:
                z[cur_par] += 1
            L = j - i + 1
            if ones == 0:
                r = 0, L
            else:
                r = ones, z[1 - cur_par], L
            classes.add(r)
    return len(classes)

✅ Code

Square Root of LCA Convolution (LCASQRT)

First let’s think of a leaf node, the only non-zero term would be itself. So, the convolution becomes \(a_x ^ 2 % M\). Now, in order to find \(a_x\), we need to take the sqrt of the given \(c_x\) (mod M). So, this suggests we can perhaps calculate these values bottom up and multiply the number of possibilities as we go up.

Let’s take a look at a node X in general: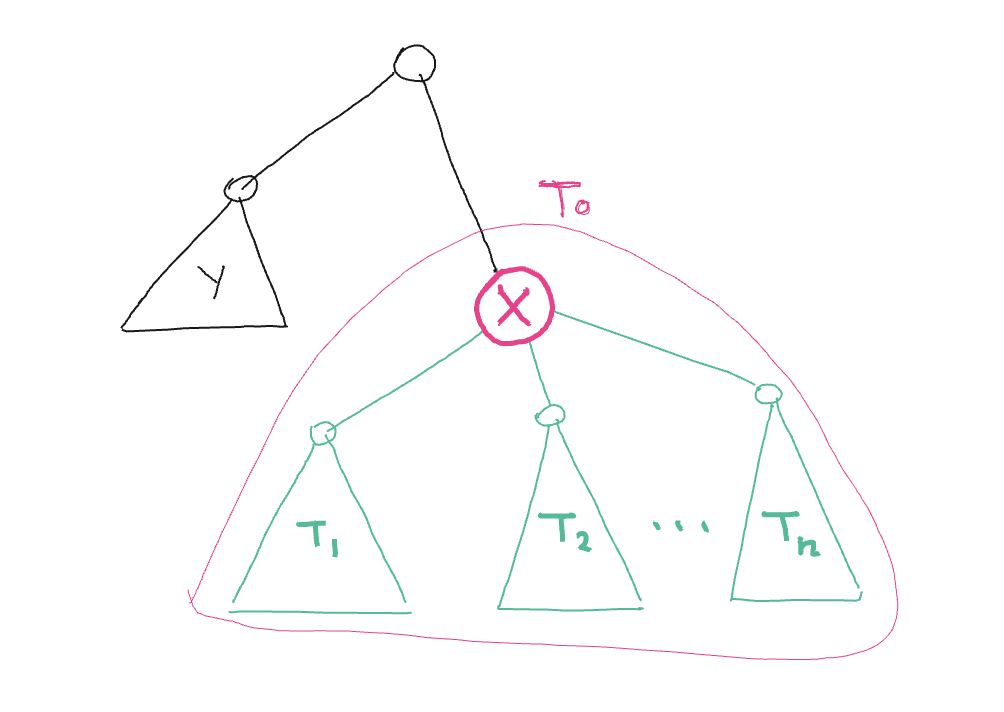

We can’t pick any node from the black area, since the LCA of that node and no other node will be \(X\). Now, if we pick a node from say \(T1\), it’s value will be multiplied with any value from \(T2\), \(T3\), … , \(Tn\) as well as \(X\) itself. Remember that we can also pick \(X\) and it will be multiplied with everything under the subtree rooted at \(X\) (i.e. \(T0\)). Doing a little bit of math, we can figure out the value of \(X\) (i.e. \(a_x\)) as you can see in my notes: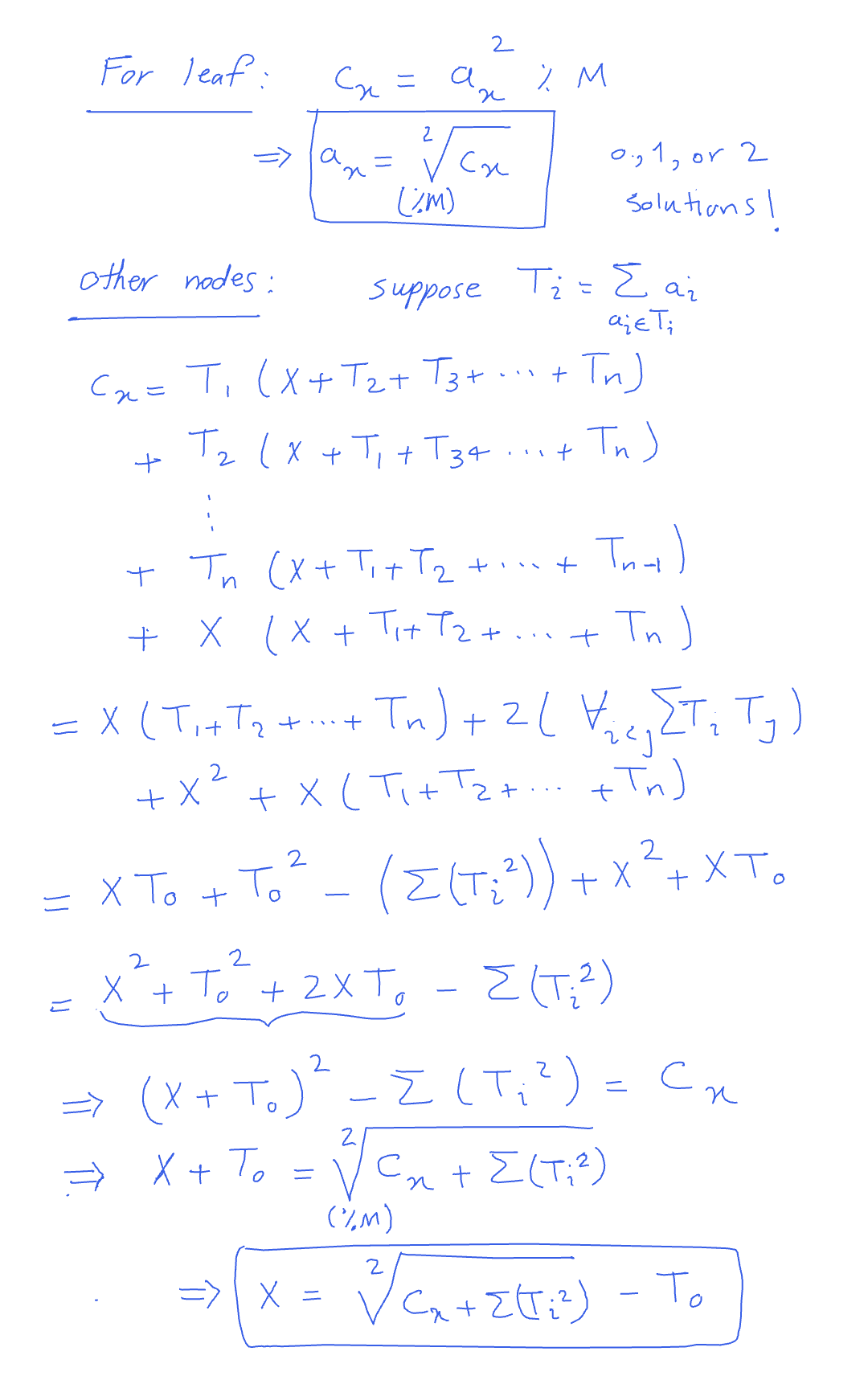

You can compute sqrt mod M efficiently using Tonelli–Shanks Algorithm and there will always be 0, 1 or 2 possible solutions. If you ever encounter 0, no answer exists to this problem. Otherwise, multiply all possible answers for each node. In order to output one such answer, just pick any of the solutions you found along the way.

Finally, in order to traverse the tree bottom-up, create the tree:

def build_tree(p):
    child = [[] for i in p]
    for i, pi in enumerate(p):
        if pi != -1:
            child[pi].append(i)
    return child

and do a topological sort:

def topo(child, cur, topo_list):
    for c in child[cur]:
        topo(child, c, topo_list)
    topo_list.append(cur)

✅ Code

Permutations (DIVPERMS)

I only managed to solve one for \(N <= 15\). You can pretty much turn any permutation counting problem with complexity \(O(N!)\) to a dynamic programming with complexity of \(O(2^N)\). You keep track of visited numbers in a bitset and consider new numbers to be added to the set. In this case, because we are interested in the consecutive divisions \(\frac{P_i}{P_{i-1}}\), we need to also store the last element of the visited set in the dp state. So, overall we have a dp state of: dp[mask][last][cost] which stores the number of permutations with the elements in mask, ending in last, with cost cost. You can calculate each entry in O(N), so your total time will be like: 2^N * N * N * N which for N=15 is about 10^8 and is doable in the given time limit.

I was lazy and memoiz’d instead of dp:

ll solve_rec(const string& t, int n, int mask, int last, int cost) {
    if ((mask - (1 << last)) == 0)
        return cost == 0 ? 1 : 0;

    ll &res = memo[mask][last][cost];
    if (res != -1) return res;

    res = 0;
    for (int i = 0; i < n; ++i) {
        if (i != last and ((1 << i) & mask) != 0) {
            res += solve_rec(t, n, mask - (1 << last), i,
                             cost - ((last + 1) % (i + 1) == 0 && t[(last + 1) / (i + 1)] == '1' ? 1 : 0));
            res %= MOD;
        }
    }
    return res;
}

✅ Code (only the first part)

If you know how to solve it for N<=40, please let me know! :)

Linear Combination (MODPARRS)

• ❌ N/A

Digit Matrix (DGMATRIX)

• ❌ N/A

Palindromic Equivalence (PALINDEQ)

• ❌ N/A