Problem

Given n and k calculate c(n, k) % 2.

O(n * k)

We can just use DP:

maxn = 1000
c = [[0] * maxn for i in range(maxn)]
for i in range(maxn):
    c[i][i] = 1
    for j in range(i):
        c[i][j] = (c[i-1][j] + c[i-1][j-1]) % 2

O(n)

Since we only want the answer mod 2. we just need to find how many 2s there are in the numerator vs. denominator of n! / (k! (n-k)!). To do that we just need to find the number of 2s in x!.

# count 2s in n!
def twos(n):
    res = 0
    t = [0] * (n+1)
    for i in range(2, n+1, 2):
        t[i] = 1 + t[i // 2]
        res += t[i]
    return res

def c(n, k):
    num = twos(n)
    den = twos(n-k) + twos(k)
    return 0 if num > den else 1  

O(log(n))

To improve the linear solution, let’s look at twos function. instead of iterating over each number in n! (1, 2, 3, …, n) let’s count how many 2s we have, then how many 4s we have, then 8s and so on (until log2(n)). This leads to a O(log(n)) solution:

# count 2s in n!
def twos(n):
    res = 0
    p = 1
    for i in range(1, n):
        if p > n:
            break
        p *= 2
        res += n // p
    return res

def c(n, k):
    num = twos(n)
    den = twos(n-k) + twos(k)
    return 0 if num > den else 1  

O(1)

Now, can we do it faster? Let’s first print out c(n, k) % 2 and look at it:

maxn = 32
for i in range(maxn):
    for j in range(i+1):
        print(c(i, j), end=' ')
    print()

Output:

Yes, this is the famous Sierpiński triangle fractal!

As you probably know, this simple code prints the Sierpiński triangle but upside down:

N = 32
for i in range(N):
    for j in range(N):
        print('0' if i & j else '1', end=' ')
    print()

Now, changing i & j to (i - j) & j would flip the triangle and we get:

This perfectly matches the triangle we got from c(n, k) % 2, which suggests the simple O(1) solution:

# c(n, k) mod 2
def c(n, k):
    return 0 if (n - k) & k else 1

Proof

Let’s take a closer look and actually prove why this simple solution works. To solve c(n, k) % 2 Let’s use Lucas’s theorem. It states that we can compute c(n, k) by breaking down n and k into their digits in base p (p needs to be prime):

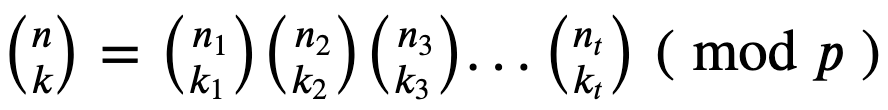
Substituting for p = 2, each digit is either 0 or 1. So:

c(0, 0) = c(1, 0) = c(1, 1) = 1

while,

c(0, 1) = 0

Now, based on Lucas’s theorem, in order for c(n, k) % 2 to be 1 all the terms on the right hand side need to be 1. This means for any set bit in k the corresponding bit in n should be set as well. In other words:

n | k == n

or

n & k == k

or

(n - k) & k == 0