Binary Indexed Tree (Fenwick Tree)

Introduction

Given an array a of n integers, we want to answer queries for sum of a range efficiently. For exmaple, for a = [2, -1, 4, 3, -5, 9], sum[2, 5) = 4 + 3 + (-5) = 2.

In order to solve this, we can compute the Prefix Sum of the array. Then any range becomes the difference between two prefix sums. Code:

# calculate prefix sum
# sum[i] = a[1] + ... + a[i]
sum[0] = 0
for i in range(1, n + 1):
    sum[i] = sum[i - 1] + a[i]

# inclusive x, y
def query(x, y):
    return sum[y] - sum[x - 1]

Preprocessing takes O(n) time and we answer every query in O(1). Pretty good!

Now we want to be able to support update queries as well! let’s assume updates are done in terms of increments and add(i, k) adds value k to a[i]. Two possible approaches:

Update the i-th element (a[i] += k) and for each query, iterate over elements in the range in O(n). Let’s call this: <O(1), O(n)>.
Add value k to all the prefix sums that contain a[i]. This would take O(n) time to update but still O(1) to query, hence <O(n), O(1)>.

Would it be possible to have a solution in between? Maybe <O(log(n)), O(log(n))>?

Binary Indexed Tree (BIT)

Binary Indexed Tree (BIT), also known as Fenwick Tree, is a data structure that provides both updates and queries in O(log(n)) time. The idea is similar to storing prefix sums. However, we store smarter ranges such that each a[i] falls into O(log(n)) ranges. Also, in order to compute pre_sum[i] we would need to sum up O(log(n)) ranges.

Note that we only solve the problem of finding sum(i) = a[1] + ... + a[i]. Using sum(i), we can answer any arbitrary sum(i, j) using the trick mentioned in the introduction section.

Structure

Although Binary Indexed Tree is a tree in concept, they are typically stored as an array. The image below shows how the tree maps to an array. On the left, you see the nodes of the tree corresponding to a bar representing the range of the array they are responsible for. On the right, is the actual array c we store in our code.

BIT

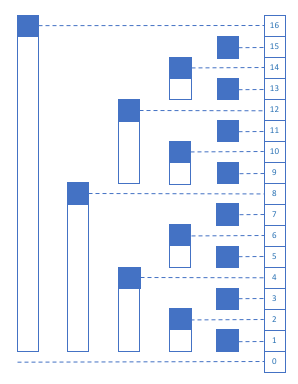
A BIT is understood by considering a 1-based array. Each element whose index i is a power of 2 contains the sum of the first i elements. Each element whose index is not a power of 2 contains the sum of the values since its parent in the tree, and that parent is found by clearing the least-significant bit in the index. (note that the x-th column from right in the image above corresponds to all indices in the array where the index of the lowest significant bit is x)

In the following sections, we look at each operation separately with an example to clarify how BIT works.

Query

Example: query for sum of all the elements up to 11.

11 in binary is 1011 which is 8 + 2 + 1. If we compute the cumulative sum of these 3 numbers, we get the indices we need to sum up, that is: [8, 8 + 2, 8 + 2 + 1] = [8, 10, 11]. So, query(11) = c[8] + c[10] + c[11]. In binary, we start with 1011 and each time we clear the least significant bit (lsb) until we reach 0.

start 1011
next 1011 - 0001 = 1010
next 1010 - 0010 = 1000

Update

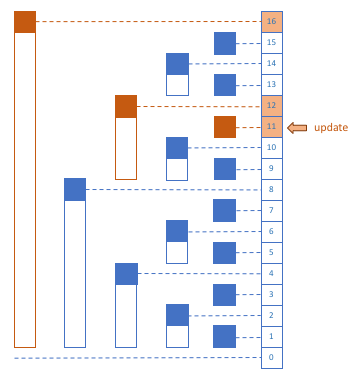
Example: increment element at 11 by some amount.

We need to update any range that contains 11. We start with 11 itself, which is 01011 in binary. In order to find the next range to the left of the current range (in the image below), we need to add 1 to the least significant bit (lsb). This gives us the smallest number greater than the current number with a higher lsb. In binary, we start with 01011 and each time we add the lsb of the number to it, until it is larger than the size of array.

start 01011
next 01011 + 00001 = 01100
next 01100 + 00100 = 10000

Code

And with these few lines of code you can solve the problem of update/query in <O(log(n)), O(log(n))>

c = [0] * (n + 1)

# get the least significant bit (ex: 1010 -> 0010)
def lsb(x):
    return x & (-x)

# get sum from 1 to i
def sum(i):
    s = 0
    while i > 0:
        s += c[i]
        i -= lsb(i)
    return s

# add k to i-th element
def add(i, inc):
    while i < len(c):
        c[i] += inc
        i += lsb(i)

Nima Aghdaii