The Chaos Game

The Sierpiński triangle is a famous fractal with many interesting properties. Here we can take a look at a fun way to generate it!

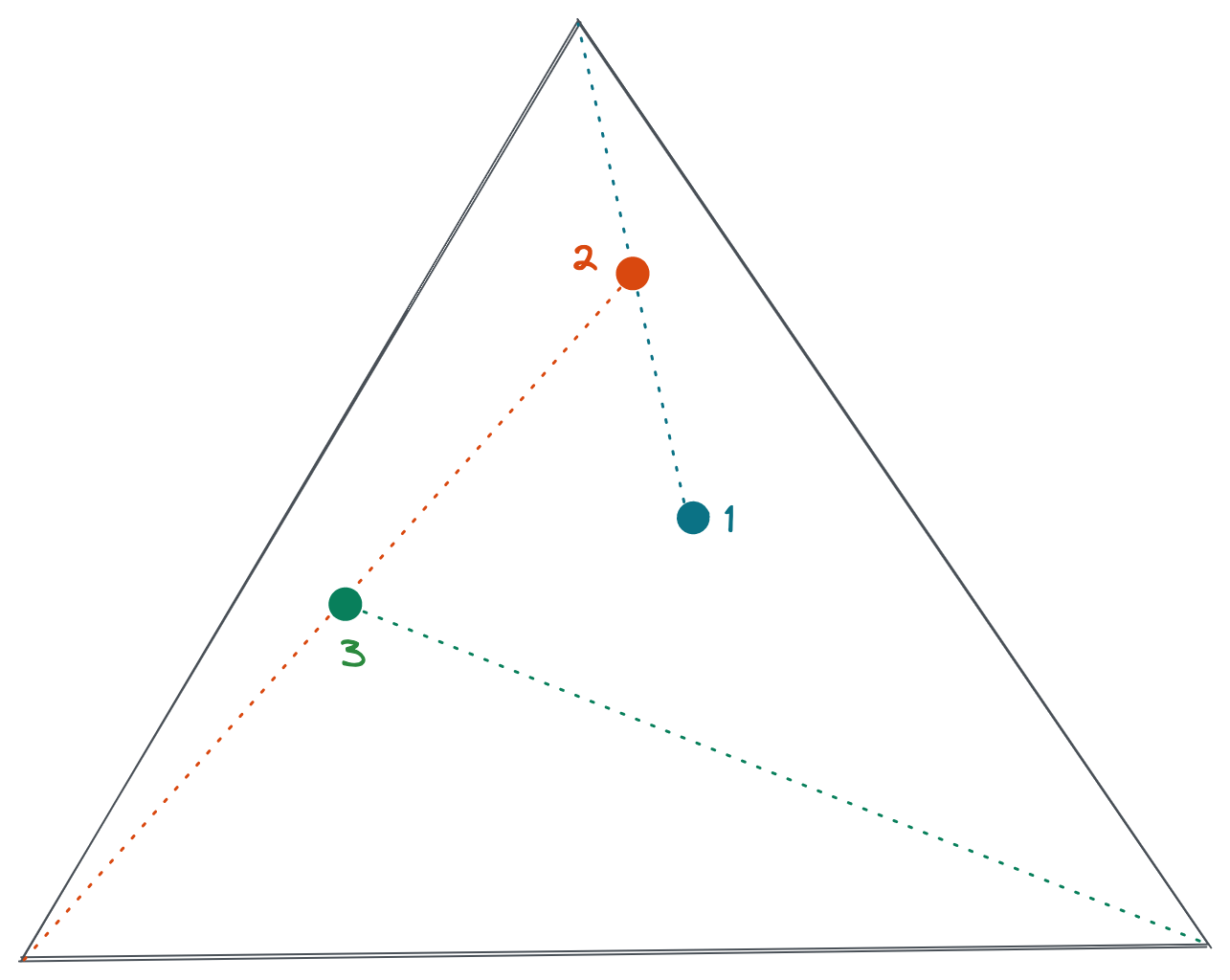
Follow these steps:

1. Start from a random point inside the triangle (P)
2. Mark P
3. Pick a random corner of the triangle (C)
4. P = the midpoint of the line segment PC
5. go to step (2)

Simulation

The simulation below demonstrates what happens if we repeat this process 2000 times.

Now, what happens if instead of the midpoint (w = 0.5) we pick the (w = 0.1) point or (w = 0.2)?

The simulation below slowly varies w from 0 to 0.5.

Discussion

Theoretical Guarantee

Theoretically, it is not guaranteed that this process would result in the Sierpinski triangle and it is easy to observe that. Imagine if we start from the center of the triangle and always pick the same corner. Even if we repeat this process forever, we will never pick any point on the Sierpinski triangle. However, you can prove that in practice it will converge to the Sierpinski triangle.

Proof of convergence

Here we just outline the proof and leave the details to you as an exercise:

1. Prove that the set of points on the Sierpinski triangle is closed under the midpoint-ing operation. In other words, prove that once you land anywhere on the Sierpinski triangle, you will never leave the triangle. (hint: pick a small inner triangle and a corner, show that this triangle maps to another smaller triangle (half the size) under the midpoint-ing operation)

2. Prove that if your point is not on the Sierpinski triangle, each time you apply the midpoint-ing operation, your distance to the closest point on the triangle will be halved (you exponentially converge to the Sierpinski triangle).

3. Prove that we have an equal likelihood to land on any point on the triangle.